Swans tile

-
Lately, I have been creating new shapes from gaps or voids which are left when placing other tiles such as Bob Nungester's gingerbread man.

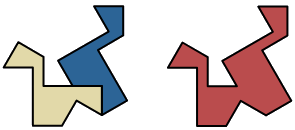
It transpires that one of these new shapes (below right) can be made up of two of Bram Cohen's computer generated 'ducks' (below left) which I have named 'swans':






Interestingly, swans can easily tile the plane in a variety of ways, displaying symmetries every which way you look.  Mirroring of the polygon doesn't work so it's effectively a single tile.

There are five ways that an 'indent' can be filled:






The first 'enclosure' (above top left) produces at least 17 different coronas (worked out by hand) and all can be expanded.  It is reasonable to assume that the other four will produce a similar number:




I added a further three coronas to one of the examples above:






This shape is most impressive when creating two or three-fold radial patterns as they are likely to be different every time.

There are three central core configurations:






Each motif can easily produce periodic tilings.  In fact, all three motifs show up in each of the three tessellations if colours are ignored.  Only points of origin change:







By rotating every alternate motif 60 degrees on the outer rings, slight variations occur.






But much more interesting patterns can also arise:






Here's another with a different arrangement.  There is often a choice to be made when placing more tiles.






Same example as above but with alterations on the right hand side to create a 'glitched' or nonuniform radial tiling.






These patterns will contain many rotational symmetries.  The top row below are the most common along with the three-fold configurations mentioned earlier.






Here's a two-fold example:






Two and three-fold symmetries commonly overlap each other.  The two disorderly patterns below are the same except for the colouring (swans in white are lone tiles):









All drawings created with Arnaud Chéritat's applet that now has grouping and multi-tile options.  And best of all, it's free for anyone to use.  

https://www.math.univ-toulouse.fr/~cheritat/AppletsDivers/Monotile/generic/v3.2/



























Comments

Post a Comment

Popular posts from this blog

Determining chess 960 starting positions with a standard die (no rethrows)

-
Image
Chess 960 is a chess game variant invented by Bobby Fischer in 1996.   In Chess 960, the pawns are lined up on the second rank as in standard chess.   The first rank pieces are positioned randomly whilst conforming to certain caveats - the king must be placed somewhere between the rooks to allow castling; the bishops must stand on opposite coloured squares. I've worked out a system that allows me to select a starting arrangement for the first rank pieces using a standard six sided die without the need for rethrows.  My dice procedure is different from that of  I ngo Althöfer's (devised in 1998), where rethrows can occur.   Some information on how his system works can be seen here https://www.chessvariants.org/diffsetup.dir/fischer-random-setup.html The die I use to generate the random piece arrangement is a standard cube/hexahedron (one of the platonic solids).  O nly five or six throws of the die are needed to formulate one of the 960 ...
Read more

The golem

-
Image
This shape which I have named the golem, was hand picked from hundreds of Spectre-like polygons (Spectroids) that were sent my way via Ortwin Schenker, Bob Nungester and Bram Cohen.   This golem has the same number of sides as the Spectre and also shares internal angles of 90, 120 and 270 degrees. Below left is the simplest of the periodic tilings.  Positioning of new tiles is forced in most cases.  That said, the pattern can deviate at any time by placing other rotations where there are choices (as shown in the example bottom right). The golem is a delight to tessellate (you can't go wrong!).  Below are a few more examples of periodic tilings.  These can be sewn together to make larger chaotic tilings with a bit of tweaking. Next up are a couple of radial patterns.  The example on the right is (I think) quite unusual in that three golem segments are pointing towards the centre whilst the other three are pointing outwards. The golem has mirror symmetry...
Read more

Fractal chevron

-
Image
I started with a chevron consisting of four equilateral triangles.  Each of those was then subdivided into nine smaller triangles, so that alternating bumps and notches could be applied to the centre of each side on the perimeter (for practical reasons I used a reverse approach, scaling up sides by a factor of three and reducing once done).  In theory, this process can continue indefinitely to produce complex fractal-like outlines.     There are left and right versions of the modified chevron, depending on which face is upward.  This means you cannot use both versions in the same tessellation.  Nine copies of each newly generated tile, can be put together to produce the next iteration.  Applying bumps and notches to even numbered polyiamonds, alters the tiling properties after the first iteration. There are four permutations for the chevron but only two for the modified versions, i.e., first and third from the left. These bumped and notched chevro...
Read more